2.10.1 Summary of Primary Constructs

Primary expressions are those that can stand alone as operands of any operator without further parenthesization. Here is a summary of primary operands in Myron.

• Integrals, integrations, derivatives, generators, piecewise expressions (except the ternary form) are all primaries.
• ⅇ, ℽ, π, ⅆ, ⅈ ,ɪ and ʈ are special symbols. Their glyphs are different from the plain letter e, the Greek letter gamma, the Greek letter pi and the letters d, i, I and t used as variables.
• ⅇ is used as a constant. It represents Euler's number, the base of the natural logarithm.
• ℽ represents the Euler-Mascheroni constant.
• ⅆ is used in integral and derivative operators as well as series generators
• ⅈ is used in constructing complex numbers.
• ɪ (entered as [1]) denotes the identity matrix whose size is determined by context.
• π represents the ratio of a circle's circumference to its diameter.
• ʈ is used to introduce transforms; as a list suffix to denote a tuple type; as an expression suffix to denote conversion to tuple.
• ∞, ¿, ⊤ and ⊥ are real constants (see Figure 2.15)
• ℙ, ℕ, ℤ, ℚ, ℝ and ℂ are special sets (see Figure 2.20 (b))
• ĉ is the constant of integration
• Ø denotes the empty set
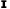
• ɪ (entered as [1]) and [0] (entered as [0]) denote the identity and zero matrices whose sizes are determined by context. They are special cases of [n] where n is a number. The general notation represents a matrix with the number on the diagonal and zeroes elsewhere whose size conforms to any matrix used as the other operand of a binary operator. For example, [r+c|r∈0, 2|c∈0, 2]×2ɪ simplifies to [(0, 2, 4), (2, 4, 6), (4, 6, 8)] and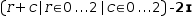 [r+c|r∈0, 2|c∈0, 2]-2ɪ simplifies to [(, -2, 1, 2), (1, 0, 3), (2, 3, 2)].
• λ by itself is a special symbol and cannot be used as a variable name nor as the first character of a variable name, although it can be used within variable names.
  • λ introduces a lambda expression, a form of anonymous function definition sometimes used as an argument.
• Builtin functions do not require parenthesis around their single argument: sin, cos, tan, cot, sec, csc, arcsin, arccos, arctan, arccot, arcsec, arccsc, log, ln, det, cof
• log as a unary operator implies base 10.
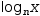
• log as a function has two parameters: log(base, expr). For example, log(n,x) displays as log(n, x).
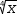
• root has two parameters: root(inverse-exponent, expr). For example, root(4,x) displays as 4√x. It can also be entered as 4√x. √x is shorthand for root(2,x).
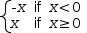
• if is followed by a multi-element list of the form conditional → expression. For example, if(x<0 → -x,x≥0 → x) displays as the piecewise expression if(x&lt;0→-x, x≥0→x).
• { and } are used to denote sets, as in {1,2,3}.
• [ and ] are used to denote matrices. A matrix contains tuples, denoted by comma-separated lists. For example, [(1,2),(3,4,5),(,0)] displays as [(1, 2, 0), (3, 4, 5), (0, 0, 0)].
• composites and collections are primaries
  • ( and ) are used to denote tuples, as in (1,2,3). Note the singleton tuple is distinguished from a simple parenthesized expression by a leading comma, as in (,0).
  • ( and ) followed by a type constant (one of ⅈ, ɽ, ʋ ʂ, ʈ or ɱ) are used to denote complex, radial, vector, set, tuple or matrix values.
• bracketing operators are treated as primaries
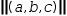
  • When | is used as parenthesis, it denotes magnitude. For scalars, magnitude produces absolute value. For collections and composites other than radials, magnitude produces a Pythagorean expression. For example, |(a, b, c)| simplifies to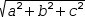 √(a^2+b^2+c^2). For radials, magnitude simply produces the length component.
  • Ceiling and floor operators are entered using the bracket pairs ⌈ ⌉ and ⌊ ⌋. An alternate form allows a closing parenthesis to complete the bracketing.